As part of my paper on falling through the centre of the Earth, I studied something called the brachistochrone curve. From the Greek for "shortest time," this is the curve that allows something to fall from point A to point B in the least amount of time. Finding this shape was posed as a challenge by Johann Bernoulli in 1696 to the leading physicists of the day, and was quickly solved by Isaac Newton, Gottfried Leibniz, and others. The solution is a shape called a cycloid, the shape traced out by a rolling circle. Apparently Albert Einstein likes to ride them, and it is the fastest shape because it has the right balance of short distance and high speed (the cycloid with the green ball wins, ignore yellow and blue).
The brachistochrone curve inside the Earth (assuming uniform density) was worked out, among others, by Venezian around 1966. The problem is more complicated because gravity now varies (linearly) with distance from the centre, and the geometry is polar rather than Cartesian. The solution is the related hypocycloid, traced by a smaller circle rolling inside a bigger circle.
Another problem that had been worked out in the literature was the brachistochrone problem around a point-mass in Newtonian gravity: polar geometry where the gravitational field decays as 1/r2. This was solved independently by a few researchers, and there isn't an analytical solution (one that can be written down as an equation), but these curves generally run deeper than the hypocycloid, because gravity is comparatively stronger towards the centre, so they can save time by going deeper. What's interesting, however, is that if two points on the surface are separated by more than 120 degrees, no such curve exists. Beyond this, it is faster just to go "down" to the centre, switch directions, and go "up" to another point, rather than taking a smooth curve. If you try to calculate the brachistochrone curves, they hit a wall, so to speak. (that image is from John Gemmer, one of the people to figure this out. His website on the problem has some neat animations.)
Because the Earth is not uniform, and is not a point-mass, I developed a model to find the brachistochrone between any two points on a sphere, with an arbitrary gravitational field inside, which is where this story begins. Ultimately this model allowed me to calculate the brachistochrone through the realistic Earth, but that is not what this post is about.
I wrote a script that would generate these curves, going from their point of maximum depth to the surface. (For those that care, it is this equation, where alpha is -n and Rd is the deepest radius, 0.5 in the gif below. It is solved with the Euler method.)
 |
| Finding the fastest path by starting at the bottom, working towards the top [while satisfying the minimization conditions]. |
As the starting point got deeper and deeper, the curves tended to get straighter, which makes sense: the fastest way through the centre of the Earth is a straight line.
 |
| Generating brachistochrones in a uniform Earth, getting deeper and deeper. The longest paths are almost straight lines. |
 |
| Generating brachistochrones around a point mass. The curves do not connect points separated by more than 120 degrees. They hit a wall as you go deeper. |
It turns out, I was. Two publications had mentioned the power-dependence of this critical angle. One was by Kiwi NASA mathematician Gary Tee, who started working on problems like this after the Apollo missions. In a footnote of one of his papers , Tee mentioned that a coworker, Ron Keam, had shown that as a function of field exponent, the critical angle is 2π/(n+1), meaning that for n=2, the critical angle is 2π/3, 120 degrees as expected. This was also shown in an undergraduate paper by John Gemmer, now at Brown, who gave an explicit derivation of this dependence by solving some nasty integrals.
So, for "sharper" fields, we expect a certain critical angle dependence, with a known formula. For "softer" fields, we expect no critical angle (or, the angle is 180 degrees). What does the full picture look like? Performing my computation of this angle, I found that it agrees with the established predictions in both limits (sharp and soft), but in the middle there is a transition that is described by neither limiting case! The established answer was wrong, and I was going to prove it and find the right answer! It was an unsolved problem in physics that was obscure enough that nobody else knew about it and simple enough that I could solve it. This is what the savvy call "low hanging fruit."
 |
| I'll call it the Klotz Gap and minstrels will sing its praise. |
So I tried to solve the unsolved problem, to find an expression for the angle dependence that agreed with my computations. I tried, but was unable to do so. I am not a very good mathematician. Tee, Gemmer, and myself all use different geometry and notation to derive the brachistochrone, so I was attempting to find an expression for this angle with my formalism, unsuccessfully. I wanted to ask Gary Tee how he and Ron Keam did it, but I don't know if he's still alive. So I found Ron Keam's email and asked him if he remembered how he contributed to a footnote in 1998. Now retired, he kindly replied saying his notes may or may not be in a big stack of papers in his attic, and mused that mathematical research serves as an effective elixir of life. Then, I tried working through Gemmer's derivation to see if he had made any approximations or Taylor series cutoffs or anything like that in order to solve the integral. There was nothing of the sort, and I was eventually to re-produce his answer. So, even though I had found that the Keam-Gemmer relation broke down in certain cases, I could not prove it.
Finally, I emailed John Gemmer to see if he minded answering some questions about something he did six years ago. He quickly got back to me and I explained the situation, explaining my results, Tee's logarithm results, and how they fit in between the two limits, and my intuition on the problem. He agreed with my intuition and found my results surprising. Then, he cleared up the discrepancy. One of the conditions for the brachistochrone is that the path is horizontal at its deepest point, and he integrated brachistochrone curves with this condition at a point very close to the origin up to the surface, making the starting point smaller and smaller. This is in effect a numerical method of replicating his derived result, which is in the limit of having the deepest point at the origin. What he found was that even for very small initial radius 10-6, his computations agreed with mine, that the Keam-Gemmer relation broke down. However, with much more intense computation, going down to a 10-20 initial radius, he showed that if you make the calculation extremely accurate you will eventually recreate the Keam-Gemmer relation for sharp fields and the no-critical-angle solution for soft fields.
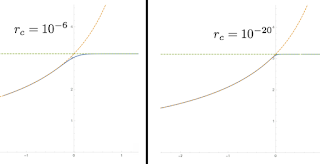 |
| The Klotz Gap vanishes. Thank you to John Gemmer for generating and giving me permission to use these images. |
The unsolved problem that I was trying to solve did not exist, and I had lacked the computational resources to prove it. What of Tee's logarithmic counterexample? A close reading of his paper points out that he had gone down to 10-8 in initial radius to do the computation, and suspected that he could bridge those extra six degrees if he went further. I should have read that paper more closely instead of just getting excited about it. Overall, it was a fun little brain teaser that I set myself on, but it turned out that the unsolved problem was actually solved.
This is really cool!
ReplyDeleteAre these hypercycloids what determine seismic wave travel paths? They're influenced by density rather than gravity, so it isn't immediately obvious to me that they would, but i imagine they could be and the shapes look about right.
I'm not exactly sure. I think they are governed by the same principles: propagating in the least amount of time given the different density layers. One of the early solutions to the brachistochrone problem essentially does this with light, asking what path light would take through many layers of varying refractive index. So I guess when a seismic wave reflects from its deepest point, it is undergoing total internal reflection.
DeleteVery interesting! Oddly enough, I always thought that the 'Klotz Gap' was the space between my two front teeth. I would love it to vanish the way yours has.
ReplyDeleteBob Klotz
Have you tried the patented Marvin Klotz Gap Removal technique?
Delete